Static Equilibrium

The special situation in which the net force on an object turns out to be zero, called static equilibrium, tells you immediately that the object isn’t accelerating. If the object is moving with some velocity, it will remain moving with that exact same velocity. If the object is at rest, it will remain at rest. Sounds familiar, doesn’t it? This is a restatement of Newton’s 1st Law of Motion, the Law of Inertia. So in reality, Newton’s 1st Law is just a special case of Newton’s 2nd Law, describing static equilibrium conditions! Consider the situation of a tug-of-war... if both participants are pulling with tremendous force, but the force is balanced, there is no acceleration -- a great example of static equilibrium.
Static equilibrium conditions are so widespread that knowing how to explore and analyze these conditions is a key stepping stone to understanding more complex situations.
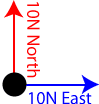
One common analysis question involves finding the equilibrant force given a free body diagram on an object. The equilibrant is a single force vector that you add to the unbalanced forces on an object in order to bring it into static equilibrium. For example, if you are given a force vector of 10N north and 10N east, and asked to find the equilibrant, you're really being asked to find a force that will offset the two given forces, bringing the object into static equilibrium.
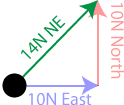
To find the equilibrant, you must first find the net force being applied to the object. To do this, we revisit our vector math and add up the two vectors by first lining them up tip to tail, then drawing a straight line from the starting point of the first vector to the ending point of the last vector. The magnitude of this vector can be found from the Pythagorean Theorem.
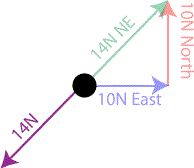
Finally, to find the equilibrant vector, add a single vector to the diagram that will give a net force of zero. If your total net force is currently 14N northeast, then the vector that should bring this back into equilibrium, the equilibrant, must be the opposite of 14N northeast, or a vector with magnitude 14N to the southwest.
Question: A 20-newton force due north and a 20-newton force due east act concurrently on an object, as shown in the diagram below.
What additional force is necessary to bring the object into a state of equilibrium?
Answer: The resultant vector is 28 newtons northeast, so its equilibrant must be 28 newtons southwest.
Another common analysis question involves being asked whether three vectors could be arranged to provide a static equilibrium situation. For example:
"Can the three vectors 5N, 8N, and 12N be in equilibrium?"
To solve a question like this, we'll walk through three easy steps.
- Add the first two vectors: 5N + 8N = 13N
- Subtract the first two vectors: 8N-5N = 3N
- If the remaining vector falls between your answers to #1 and #2, you can have an equilibrium situation if the vectors are lined up properly.
In this case, then, 5N, 8N, and 12N can be in equilibrium. Test yourself by proving that the force vectors 5N, 6N, and 12N cannot be in equilibrium. Let's try a problem from the June 2006 NY Regents Physics Exam:
Question: Which body is in equilibrium?
- a satellite orbiting Earth in a circular orbit
- a ball falling freely toward the surface of Earth
- a car moving with constant speed along a straight, level road
- a projectile at the highest point in its trajectory
Answer: (3) a car moving with constant speed.


