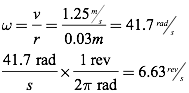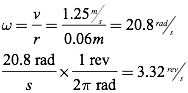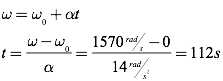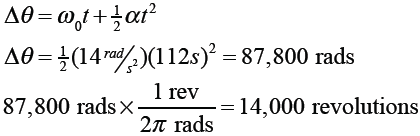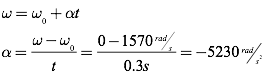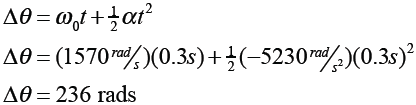Honors Physics - Rotational Kinematics
Radians and Degrees
Typically people discuss rotational motion in terms of degrees, where one entire rotation around a circle is equal to 360°. When dealing with rotational motion from a physics perspective, measuring rotational motion in units known as radians (rads) is much more efficient. A radian measures a distance around an arc equal to the length of the arc’s radius.
Up to this point, you’ve described distances and displacements in terms of Δx and Δy. In discussing angular displacements, you must transition to describing the translational displacement around an arc in terms of the variable s, while continuing to use the symbol θ (theta) to represent angles and angular displacement.
The distance completely around a circular path (360°), known as the circumference, C, can be found using ∆s = C = 2𝜋r = 2𝜋 radians. Therefore, you can use this as a conversion factor to move back and forth between degrees and radians.
Question: Convert 90° to radians.
Answer:
Question: Convert 6 radians to degrees.
Answer:
Angles are also measured in terms of revolutions (complete trips around a circle). A complete single rotation is equal to 360°, therefore you can write the conversion factors for rotational distances and displacements as 360° = 2𝜋 radians = 1 revolution.
Question: Convert 1.5 revolutions to both radians and degrees.
Answer:
Velocity and Acceleration
Rotational kinematics is extremely similar to translational kinematics, all you have to do is learn the rotational versions of the kinematic variables and equations. When you learned translation kinematics, displacement was discussed in terms of Δx. With rotational kinematics, you’ll use the angular coordinate θ instead. When average velocity was introduced in the translational world, you used the formula:
![]()
When exploring rotational motion, you’ll talk about the angular velocity ω (omega), given in units of radians per second (rad/s). Because angular (rotational) velocity is a vector, define the positive direction of rotation as counter-clockwise around the circular path, and the negative direction as clockwise around the path.

![]()
NOTE: Formally, the direction of angular vectors is determined by the right-hand rule. Wrap the fingers of your right hand in the direction of the rotational displacement, velocity, or acceleration, and your thumb will point in the vector’s direction.

Question: A record spins on a phonograph at 33 rpms (revolutions per minute) clockwise. Find the angular velocity of the record.
Answer:
Note that the angular velocity vector is negative because the record is rotating in a clockwise direction.
Question: Find the magnitude of Earth’s angular velocity in radians per second.
Answer: Realizing that the Earth makes one complete revolution every 24 hours, we can estimate the magnitude of the Earth’s angular velocity as:
In similar fashion, when you learned about translational acceleration, you found acceleration as the rate of change of an object’s translational velocity:
![]()
Angular acceleration α (alpha), given in units of radians per second2, is the rate of change of an object’s angular velocity. Since angular acceleration is a vector as well, you can define its direction as positive for increasing angular velocities in the counter-clockwise direction, and negative for increasing angular velocities in the clockwise direction.
![]()
Question: A frog rides a unicycle. If the unicycle wheel begins at rest, and accelerates uniformly in a counter-clockwise direction to an angular velocity of 15 rpms in a time of 6 seconds, find the angular acceleration of the unicycle wheel.
Answer: First, convert 15 rpms to rads/s.
Next, use the definition of angular acceleration.
Again, note the positive angular acceleration, as the bicycle wheel is accelerating in the counter-clockwise direction.
Rotational Variables
Putting these definitions together, you observe a very strong parallel between translational kinematic quantities and rotational kinematic quantities.
| Variable | Translational | Angular |
|---|---|---|
| Displacement | Δs |
Δθ |
| Velocity | v |
ω |
| Acceleration | a |
α |
| Time | t |
t |
It’s quite straightforward to translate between translational and angular variables as well when you know the radius (r) of the point of interest on a rotating object.
Question: A knight swings a mace of radius 1m in two complete revolutions. What is the translational displacement of the mace?
Answer:
Question: A compact disc player is designed to vary the disc’s rotational velocity so that the point being read by the laser moves at a linear velocity of 1.25 m/s. What is the CD’s rotational velocity in revs/s when the laser is reading information on an inner portion of the disc at a radius of 0.03m?
Answer:
Question: What is the rotational velocity of the compact disc in the previous problem when the laser is reading the outermost portion of the disc (radius=0.06m)?
Answer:
Rotational Kinematic Equations
The parallels between translational and rotational motion go even further. You developed a set of kinematic equations for translational motion that allowed you to explore the relationship between displacement, velocity, and acceleration. You can develop a corresponding set of relationships for angular displacement, angular velocity, and angular acceleration. The equations follow the same form as the translational equations, all you have to do is replace the translational variables with rotational variables, as shown in the following table.

The rotational kinematic equations can be used the same way you used the translational kinematic equations to solve problems. Once you know three of the kinematic variables, you can always use the equations to solve for the other two.

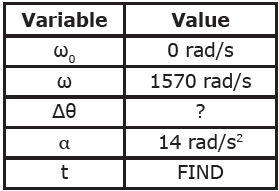
Question: A carpenter cuts a piece of wood with a high powered circular saw. The saw blade accelerates from rest with an angular acceleration of 14 rad/s2 to a maximum speed of 15,000 rpms. What is the maximum speed of the saw in radians per second?
Answer:
Question: How long does it take the saw to reach its maximum speed?
Answer: You can use the rotational kinematic equations to solve this problem:
Question: How many complete rotations does the saw make while accelerating to its maximum speed?
Answer:
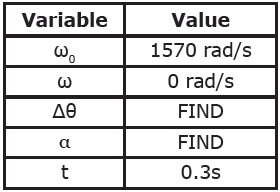
Question: A safety mechanism will bring the saw blade to rest in 0.3 seconds should the carpenter’s hand come off the saw controls. What angular acceleration does this require? How many complete revolutions will the saw blade make in this time?
Answer: Begin by re-creating the rotational kinematics table.
First find the angular acceleration.
Next, find the angular displacement.
Finally, convert the angular displacement into revolutions.