Regents Physics - Parallel Circuits

Another basic circuit type is the parallel circuit, in which there is more than one current path. To analyze resistors in a series circuit, we found an equivalent resistance. We'll follow the same strategy in analyzing resistors in parallel.

Resistors in Parallel

Let's look at a circuit made of the same components we used in our exploration of series circuits, but now we'll connect our components so as to provide multiple current paths, creating a parallel circuit.

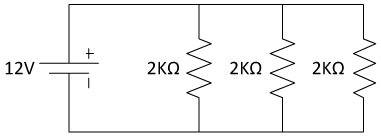
Notice that in this circuit, electricity can follow one of three different paths through each of the resistors. In many ways, this is similar to a river branching into three different smaller rivers. Each resistor, then, causes a potential drop (analogous to a waterfall), then the three rivers recombine before heading back to the battery, which we can think of like a pump, raising the river to a higher potential before sending it back on its looping path.

We can find the equivalent resistance of resistors in parallel using the formula:

Take care in using this equation, as it's easy to make errors in performing your calculations. Let's see if we can find the equivalent resistance for our sample circuit.

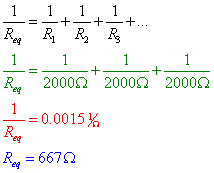
Circuit Analysis

We can once again utilize a VIRP table to analyze our circuit, beginning by filling in what we know directly from the circuit diagram.

VIRP Table

	V	I	R	P
R1			2000
R2			2000
R3			2000
Total	12V

We can also see from the circuit diagram that the potential drop across each resistor must be 12V, since the ends of each resistor are held at a 12V difference by the battery.

VIRP Table

	V	I	R	P
R1	12V		2000
R2	12V		2000
R3	12V		2000
Total	12V

Next, we can fill in the current through each of the individual resistors since we know the voltage drop across each resistor using Ohm's Law (I=V/R) to find I=0.006A.

VIRP Table

	V	I	R	P
R1	12V	0.006A	2000
R2	12V	0.006A	2000
R3	12V	0.006A	2000
Total	12V

Using Kirchhoff's Current Law, we can see that if 0.006A flows through each of the resistors, these currents all come together to form a total current of 0.018A.

VIRP Table

	V	I	R	P
R1	12V	0.006A	2000
R2	12V	0.006A	2000
R3	12V	0.006A	2000
Total	12V	0.018A

Because each of the three resistors has the same resistance, it only makes sense that the current would be split evenly between them. And we can confirm our earlier calculation about the equivalent resistance by calculating the total resistance of the circuit using Ohm's Law: .

VIRP Table

	V	I	R	P
R1	12V	0.006A	2000
R2	12V	0.006A	2000
R3	12V	0.006A	2000
Total	12V	0.018A	667

Finally, we can finish our VIRP table using any of the three applicable equations for power dissipation to find:

VIRP Table

	V	I	R	P
R1	12V	0.006A	2000	0.072W
R2	12V	0.006A	2000	0.072W
R3	12V	0.006A	2000	0.072W
Total	12V	0.018A	667	0.216W

Note that for resistors in parallel, the equivalent resistance is always less than the resistance of any of the individual resistors. The potential difference across each of the resistors in parallel is the same, and the current through each of the resistors adds up to the total current. This is summarized for you on the reference table:

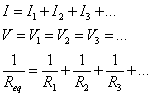
Sample Problems

Let's take a look at a basic parallel circuit analysis problem:

In similar fashion, we should also be able to construct circuit diagrams from descriptions of the circuit:

Let's take a look at a final sample problem, this time involving the use of ammeters in the analysis of our parallel circuit: