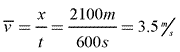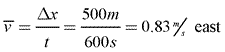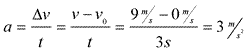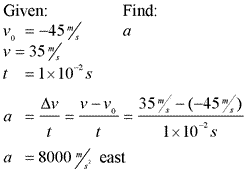Honors Physics - Defining Motion

Distance and Displacement

An object's position refers to its location at any given point in time. Position is a vector, and its magnitude is given by the symbol x. If we confine our study to motion in one dimension, we can define how far an object travels from its initial position as its distance. Distance, as defined by physics, is a scalar. It has a magnitude, or size, only. The basic unit of distance is the meter (m).

 

Sample Problem:  On a sunny afternoon, a deer walks 1300 meters east to a creek for a drink.  The deer then walks 500 meters west to the berry patch for dinner, before running 300 meters west when startled by a loud raccoon.  What distance did the deer travel?

Answer: The deer traveled 1300m + 500m + 300m, for a total distance traveled of 2100m.

 

Besides distance, in physics it is also helpful to know how far an object is from its starting point, or its change in position. The vector quantity displacement (x-x₀) describes how far an object is from its starting point, and the direction of the displacement vector points from the starting point to the finishing point. Like distance, the units of displacement are meters.

Sample Problem: A deer walks 1300 m east to a creek for a drink.  The deer then walked 500 m west to the berry patch for dinner, before running 300 m west when startled by a loud raccoon.  What is the deer’s displacement?

Answer: The deer’s displacement was 500m east.

 

Notice how for the exact same motion, distance and displacement have significantly different values. Understanding the similarities (and differences) between these concepts is an important step toward understanding kinematics.

 

Speed and Velocity

Knowing only an object's distance and displacement doesn't tell the whole story. Going back to the deer example, there's a significant difference in the picture of the deer's afternoon if the deer's travels occurred over 5 minutes 300 seconds) as opposed to over 50 minutes (3000 seconds).

How exactly does the picture change? In order to answer that question, you'll need to understand some new concepts – average speed and average velocity.

Average speed, given the symbol , is defined as distance traveled divided by time, and it tells you the rate at which an object's distance traveled changes. When applying the formula, you must make sure that x is used to represent distance traveled.

 

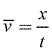
Sample Problem: A deer walks 1300 m east to a creek for a drink. The deer then walked 500 m west to the berry patch for dinner, before running 300 m west when startled by a loud raccoon. What is the deer's average speed if the entire trip took 600 seconds (10 minutes)?

Answer:

 

Average velocity, also given the symbol , is defined as displacement, or change in position, over time. It tells you the rate at which an object's displacement, or position, changes. To calculate the vector quantity average velocity, you divide the vector quantity displacement by time.

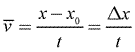
Sample Problem: A deer walks 1300 m east to a creek for a drink. The deer then walked 500 m west to the berry patch for dinner, before running 300 m west when startled by a loud raccoon. What is the deer's average velocity if the entire trip took 600 seconds (10 minutes)?

Answer:

Again, notice how we get very different answers for average speed compared to average velocity… the difference is realizing that distance and speed are scalars, and displacement and velocity are vectors. One way to help you remember these: speed is a scalar, and velocity is a vector.

 

Sample Problem: Chuck the hungry squirrel travels 4m east and 3m north in search of an acorn.  The entire trip takes him 20 seconds.  Find: Chuck’s distance traveled, Chuck’s displacement, Chuck’s average speed, and Chuck’s average velocity.

Answer:

 

Let's try another sample problem to demonstrate the potential applications of these definitions.

Sample Problem: On a highway, a car is driven 80 kilometers during the first 1.00 hour of travel, 50 kilometers during the next 0.50 hour, and 40 kilometers in the final 0.50 hour. What is the car's average speed for the entire trip?
(1) 45 km/h
(2) 60 km/h
(3) 85 km/h
(4) 170 km/h

Answer: (3)

 

Acceleration

So you’re starting to get a pretty good understanding of motion.  But what would the world be like if velocity never changed?  Objects at rest would remain at rest.  Objects in motion would remain in motion at a constant speed and direction.  And kinetic energy would never change (remember ?)  It’d make for a pretty boring world.  Thankfully, velocity can change, and this change in velocity leads to an acceleration.

More accurately, acceleration is the rate at which velocity changes.  You can write this as:

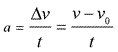
This indicates that the change in velocity divided by the time interval gives you the acceleration. Much like displacement and velocity, acceleration is a vector – it has a direction. Further, the units of acceleration are meters per second per second, or [m/s²]. Although it sounds complicated, all the units mean is that velocity changes at the rate of one meter per second, every second. So an object starting at rest and accelerating at 2 m/s² would be moving at 2 m/s after one second, 4 m/s after two seconds, 6 m/s after 3 seconds, and so on.

Of special note is the symbolism for v.  The delta symbol () indicates a change in a quantity, which is always the initial quantity subtracted from the final quantity.  For example:

 

Sample Problem: Monty the Monkey accelerates uniformly from rest to a velocity of 9 m/s in a time span of 3 seconds. Calculate Monty's acceleration.

Answer:

 

The definition of acceleration can be rearranged to provide a relationship between velocity, acceleration and time as follows:

 

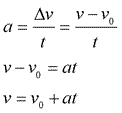
Sample Problem: The instant before a batter hits a 0.14-kilogram baseball, the velocity of the ball is 45 meters per second west. The instant after the batter hits the ball, the ball's velocity is 35 meters per second east. The bat and ball are in contact for 1.0×10^-2 second. Determine the magnitude and direction of the average acceleration of the baseball while it is in contact with the bat.

Answer:

 

Because acceleration is a vector and has direction, it's important to realize that positive and negative values for acceleration indicate direction only. Take a look at some examples. First, an acceleration of zero implies an object moves at a constant velocity. In the animation below, the car moves to the right with a constant velocity (zero acceleration).

Now, if the car starts at rest and accelerates to the right, the car speeds up as it moves to the right.

But what happens if the car starts with a velocity to the right, and accelerates to the left? The car will slow down as it moves to the right until its velocity becomes zero, then speed up as it continues accelerating to the left.

Positive accelerations don't necessarily indicate an object speeding up, and negative accelerations don't necessarily indicate an object slowing down. In one dimension, for example, if you call east the positive direction, a negative acceleration would indicate an acceleration vector pointing to the west. If the object is moving to the east (has a positive velocity), the negative acceleration would indicate the object is slowing down. If, however, the object is moving to the west (has a negative velocity), the negative acceleration would indicate the object is speeding up as it moves west.

Exasperating, isn't it? Putting it much more simply, if acceleration and velocity have the same sign (vectors in the same direction), the object is speeding up. If acceleration and velocity have opposite signs (vectors in opposite directions), the object is slowing down.