Free Body Diagrams

Fortunately, we have a terrific tool for analyzing the forces acting upon objects. This tool is known as a free body diagram. Quite simply, a free body diagram is a representation of a single object, or system, with vector arrows showing all the external forces acting on the object. These diagrams make it very easy to identify exactly what the net force is on an object, and they’re also quite simple to create:

1. Isolate the object of interest. Draw the object as a point particle representing the same mass.
2. Sketch and label each of the external forces acting on the object.
3. Choose a coordinate system, with the direction of motion as one of the positive coordinate axes.
4. If all forces do not line up with your axes, resolve those forces into components using trigonometry (note that the formulas below only work if the angle is measured from the horizontal).
   
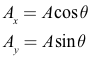
5. Redraw your free body diagram, replacing forces that don’t overlap the coordinates axes with their components.

 

As an example, picture a glass of soda sitting on the dining room table. You can represent the glass of soda in the diagram as a single dot. Then, represent each of the vector forces acting on the soda by drawing arrows and labeling them. In this case, you can start by recognizing the force of gravity on the soda, known more commonly as the soda’s weight. Although you could label this force as F_grav, or W, get in the habit right now of writing the force of gravity on an object as mg. You can do this because the force of gravity on an object is equal to the object’s mass times the acceleration due to gravity, g.

 

Of course, since the soda isn’t accelerating, there must be another force acting on the soda to balance out the weight. This force, the force of the table pushing up on the soda, is known as the normal force (F_N). In physics, the normal force refers to a force perpendicular to a surface (normal in this case meaning perpendicular). The force of gravity on the soda must exactly match the normal force on the soda, although they are in opposite directions, therefore there is no net force on the soda. The free body diagram for this situation could be drawn as shown at right.

 

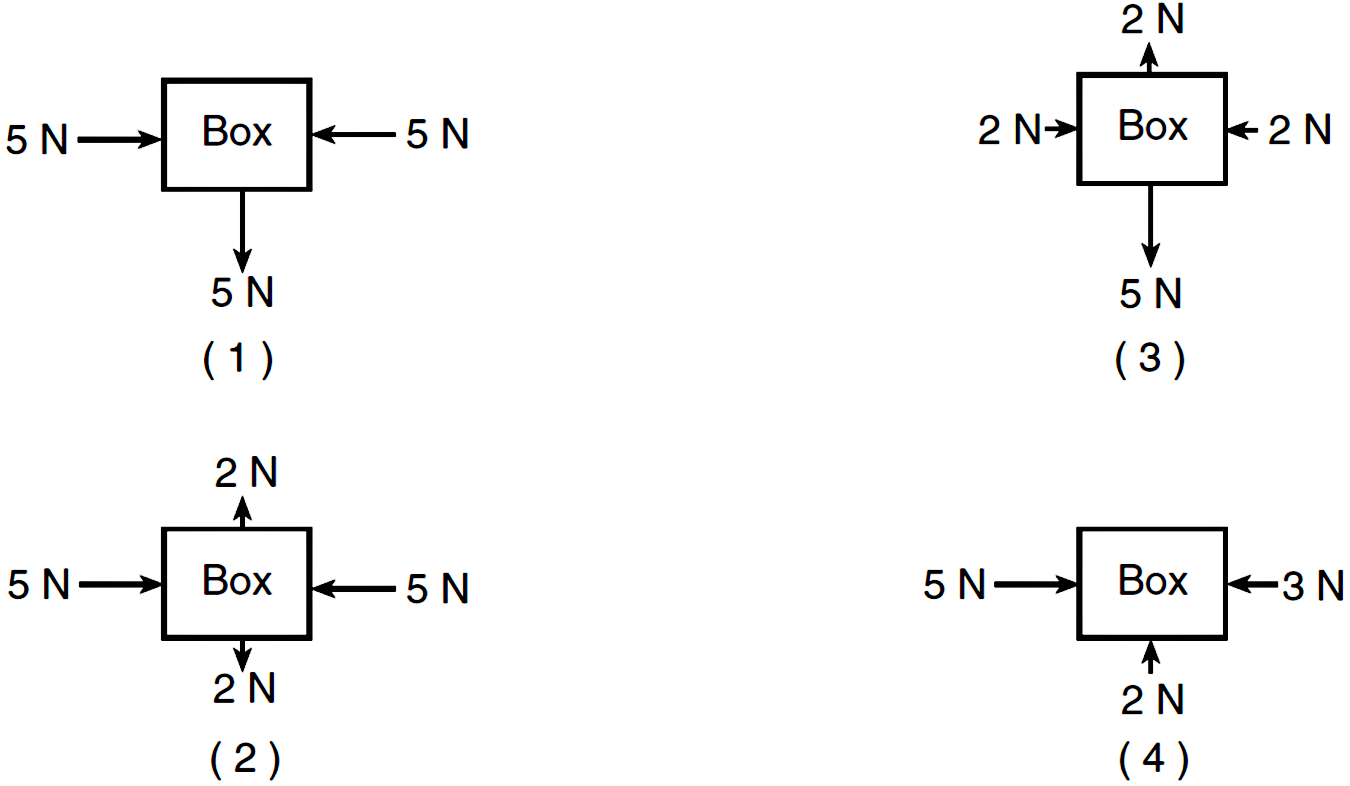
Question: Which diagram represents a box in equilibrium?

Answer: (2) all forces are balanced for a net force of zero.

 

 

Question: If the sum of all the forces acting on a moving object is zero, the object will

1. slow down and stop
2. change the direction of its motion
3. accelerate uniformly
4. continue moving with constant velocity

Answer: (4) continue moving with constant velocity in accordance with Newton’s 1st Law of Motion.