Wave Interference

Superposition

When more than one wave travels through the same location in the same medium at the same time, the total displacement of the medium is governed by the principle of superposition. The principle of superposition simply states that the total displacement is the sum of all the individual displacements of the waves. The combined effect of the interaction of the multiple waves is known as wave interference.

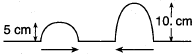
Question: The diagram shows two pulses approaching each other in a uniform medium. Diagram the superposition of the two pulses.

Answer:

 

Constructive Interference

When two or more pulses with displacements in the same direction interact, the effect is known as constructive interference. The resulting displacement is greater than the original individual pulses. Once the pulses have passed by each other, they continue along their original path in their original shape, as if they had never met. An animation of two pulses interfering constructively is shown below.

Notice the top pulse travels to the right with a positive displacement, while the middle pulse travels to the left with a positive displacement. When the two pulses meet (shown at bottom), the interfere constructively before continuing on their path as if they had never met.

 

Destructive Interference

When two or more pulses with displacements in opposite directions interact, the effect is known as destructive interference. The resulting displacements negate each other. Once the pulses have passed by each other, they continue along their original path in their original shape, as if they had never met. An animation of two pulses interfering destructively is shown below.

Notice the top pulse travels to the right with a positive displacement, while the middle pulse travels to the left with a negative displacement. When the two pulses meet (shown at bottom), the interfere destructively before continuing on their path as if they had never met.

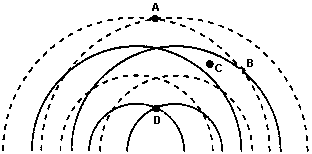
Question: Two wave sources operating in phase in the same medium produce the circular wave patterns shown in the diagram. The solid lines represent wave crests and the dashed lines represent wave troughs. Which point is at a position of maximum destructive interference?

Answer: Point B is at a position of maximum destructive interference, since point B represents the intersection of a crest and a trough.

 

 

 

Standing Waves

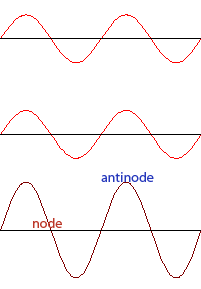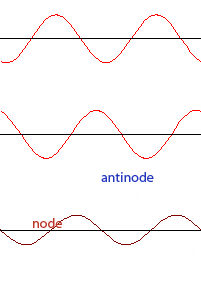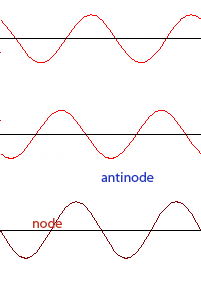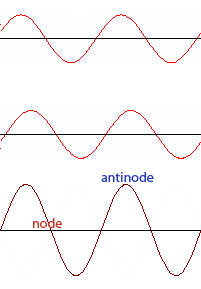
When waves of the same frequency and amplitude traveling in opposite directions meet, a standing wave is produced. A standing wave is a wave in which certain points (nodes) appear to be standing still and other points (anti-nodes) vibrate with maximum amplitude above and below the axis.

Looking at the standing wave produced on the right, we can see a total of five nodes in the wave, and four anti-nodes. For any standing wave pattern, you will always have one more node than anti-node.

Standing waves can be observed in a variety of patterns and configurations, and are responsible for the functioning of most musical instruments. Guitar strings, for example, demonstrate a standing wave pattern. By fretting the strings, you adjust the wavelength of the string, and therefore the frequency of the standing wave pattern, creating a different pitch. Similar functionality is seen in instruments ranging from pianos and drums to flutes, harps, trombones, xylophones, and even pipe organs!

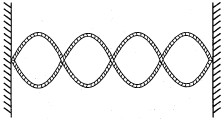
Question: The diagram shows a standing wave in a string clamped at each end. What is the total number of nodes and antinodes in the standing wave?

Answer: Five nodes and four anti-nodes.