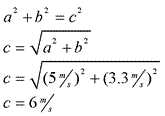Honors Physics - Math Review

Significant Figures

Significant Figures (or sig figs, for short) represent a manner of showing which digits in a number are known to some level of certainty. But how do we know which digits are significant? There are some rules to help us with this. If we start with a number in scientific notation:

• All non-zero digits are significant.
• All digits between non-zero digits are significant.
• Zeroes to the left of significant digits are not significant.
• Zeroes to the right of significant digits are significant.

When you make a measurement in physics, you want to write what you measured using significant figures. To do this, write down as many digits as you are absolutely certain of, then take a shot at one more digit as accurately as you can. These are your significant figures.

Question: How many significant figures are in the value 43.74 km?

Answer: 4 (four non-zero digits)

 

Question: How many significant figures are in the value 4302.5 g?

Answer: 5 (All non-zero digits are significant and digits between non-zero digits are significant.)

 

Question: How many significant figures are in the value 0.0083s?

Answer: 2 (All non-zero digits are significant. Zeroes to the left of significant digits are not significant.)

 

Question: How many significant figures are in the value 1.200×10³ kg?

Answer: 4 (Zeroes to the right of significant digits are significant.)

Scientific Notation

Although physics and mathematics aren't the same thing, they are in many ways closely related. Just like English is the language of this content, mathematics is the language of physics. A solid understanding of a few simple math concepts will allow us to communicate and describe the physical world both efficiently and accurately.

Because measurements of the physical world vary so tremendously in size (imagine trying to describe the distance across the United States in units of hair thicknesses), physicists often times use what is known as scientific notation to denote very large and very small numbers. These very large and very small numbers would become quite cumbersome to write out repeatedly. Imagine writing 4,000,000,000,000 over and over again. Your hand would get tired and your pen would rapidly run out of ink! Instead, it's much easier to write this number as 4×10¹². See how much easier that is? Or on the smaller scale, the thickness of the insulating layer (known as a gate dielectric) in the integrated circuits that power our computers and other electronics can be less than 0.000000001 m. It's easy to lose track of how many zeros you have to deal with, so scientists instead would write this number as 1×10^-9 m. See how much simpler life can be with scientific notation?

Scientific notation follows these simple rules. Start by showing all the significant figures in the number you're describing, with the decimal point after the first significant digit. Then, show your number being multiplied by 10 to the appropriate power in order to give you the correct value.

It sounds more complicated than it is. Let's say, for instance, you want to show the number 300,000,000 in scientific notation (a very useful number in physics), and let's assume we know this value to three significant digits. We would start by writing our three significant digits, with the decimal point after the first digit, as "3.00". Now, we need to multiply this number by 10 to some power in order to get back to our original value. In this case, we multiply 3.00 by 10⁸, for an answer of 3.00×10⁸. Interestingly, the power you raise the 10 to is exactly equal to the number of digits you moved the decimal to the left as you converted from standard to scientific notation. Similarly, if you start in scientific notation, to convert to standard notation, all you have to do is remove the 10⁸ power by moving the decimal point eight digits to the right. Presto, you're an expert in scientific notation!

But, what do you do if the number is much smaller than one? Same basic idea… let's assume we're dealing with the approximate radius of an electron, which is 0.00000000000000282 m. It's easy to see how unwieldy this could become. We can write this in scientific notation by writing our three significant digits, with the decimal point after the first digit, as "2.82." Again, we multiply this number by some power to 10 in order to get back to our original value. Because our value is less than 1, we need to use negative powers of 10. If we raise 10 to the power -15, specifically, we get a final value of 2.82×10^-15 m. In essence, for every digit we moved the decimal place, we add another power of 10. And if we start with scientific notation, all we do is move the decimal place left one digit for every negative power of 10.

Question: Express the number 0.000470 in scientific notation.

Answer: 4.70×10^-4

 

Question: Express the number 2,870,000 in scientific notation.

Answer: 2.87×10⁶

 

Question: Expand the number 9.56×10^-3.

Answer: 0.00956

 

Question: Expand the number 1.11×10⁷.

Answer: 11,100,000

 

 

Metric System

Physics involves the study, prediction, and analysis of real-world phenomena. To communicate data accurately, we must set specific standards for our basic measurements. The physics community has standarized on what is known as the Système International (SI), which defines seven baseline measurements and their standard units, forming the foundation of what is called the metric system of measurement. The SI system is oftentimes referred to as the mks system, as the three most common measurement units are meters, kilograms, and seconds, which we'll focus on for the majority of this course. The fourth SI base unit we'll use in this course, the ampere, will be introduced in the current electricity section.

The base unit of length in the metric system, the meter, is roughly equivalent to the English yard. For smaller measurements, the meter is divided up into 100 parts, known as centimeters, and each centimeter is made up of 10 millimeters. For larger measurements, the meter is grouped into larger units of 1000 meters, known as a kilometer. The length of a baseball bat is approximately one meter, the radius of a U.S. quarter is approximately a centimeter, and the diameter of the metal in a wire paperclip is roughly one millimeter.

The base unit of mass, the kilogram (kg), is roughly equivalent to two U.S. pounds. A cube of water 10cm × 10cm × 10cm has a mass of 1 kg. Kilograms can also be broken up into larger and smaller units, with commonly used measurements of grams (1/1000th of a kilogram) and milligrams (1/1000th of a gram). The mass of a textbook is approximately 2 to 3 kilograms, the mass of a baseball is approximately 145 grams, and the mass of a mosquito is 1 to 2 milligrams.

The base unit of time, the second, is likely already familiar. Time can also be broken up into smaller units such as milliseconds (10^-3 seconds), microseconds (10^-6 seconds), and nanoseconds (10^-9 seconds), or grouped into larger units such as minutes (60 seconds), hours (60 minutes), days (24 hours), and years (365.25 days).

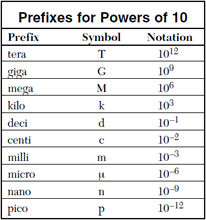
The metric system is based on powers of 10, allowing for easy conversion from one unit to another. A chart showing the meaning of commonly used metric prefixes and their notations can be extremely valuable in performing unit conversions.

Converting from one unit to another can be accomplished in a straightforward manner if you follow the described procedure:

1. Write your initial measurement with units as a fraction over 1.
2. Multiply your initial fraction by a second fraction, with a numerator (top number) having the units you want to convert to, and the denominator (bottom number) having the units of your initial measurement.
3. For any units on the top right-hand side with a prefix, determine the value for that prefix. Write that prefix in the right-hand denominator. If there is no prefix, use 1.
4. For any units on the right-hand denominator with a prefix, write the value for that prefix in the right-hand numerator. If there is no prefix, use 1.
5. Multiply through the problem, taking care to accurately record units. You should be left with a final answer in the desired units.

Let's take a look at a sample unit conversion:

 

Accuracy & Precision

When making measurements of physical quantities, how close the measurement is to the actual value is known as the accuracy of the measurement. Precision, on the other hand, is the repeatability of a measurement. A common analogy involves an archer shooting arrows at the target. The bullseye of the target represents the actual value of the measurement.

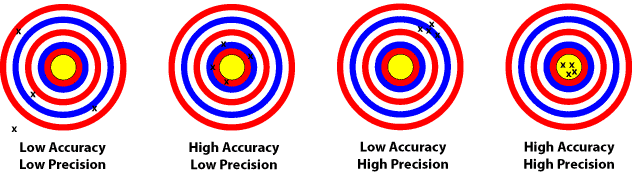
Ideally, measurements in physics should be both accurate and precise.

 

Algebra and Trigonometry

Just as we find the English language a convenient tool for conveying thoughts to each other, we need a convenient language for conveying our understanding of the world around us in order to understand its behavior. The language most commonly (and conveniently) used to describe the natural world is mathematics. Therefore, to understand physics, we need to be fluent in the mathematics of the topics we'll study in this course… specifically basic algebra and trigonometry.

Now don't you fret or frown, for those whom the word "trig" conjures up feelings of pain, angst, and frustration, have no fear. We will need only the most basic of algebra and trigonometry knowledge in order to successfully solve a wide range of physics problems.

A vast majority of problems requiring algebra can be solved using the same problem solving strategy. First, analyze the problem and write down what you know, what you need to find, and make a picture or diagram to better understand the problem if it makes sense. Then, start your solution by searching for a path that will lead you from your givens to your finds. Once you've determined an appropriate pathway (and there may be more than one), solve your problem algebraically for your answer. Finally, as your last steps, substitute in any values with units into your final equation, and solve for your answer, with units.

Our use of trigonometry, the study of right triangles, can be distilled down to the definitions of the three basic trigonometric functions. When you know the length of two sides of a right triangle, or the length of one side and a non-right angle, you can solve for all the angles and sides of the triangle.If you can use the definitions of the sine, cosine, and tangent, you'll be fine in this course.

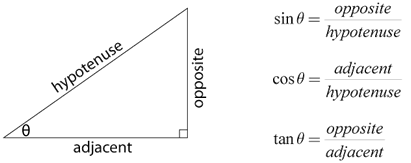
Of course, if you need to solve for the angles themselves, you can use the inverse trigonometric functions.

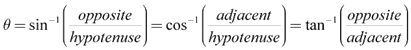
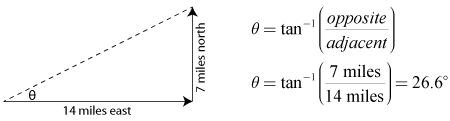
Question: A car travels from the airport 14 miles east and 7 miles north to its destination. What direction should a helicopter fly from the airport to reach the same destination, traveling in a straight line?

Answer:

 

Vectors and Scalars

Quantities in physics are used to represent real-world measurements, and therefore physicists use these quantities as tools to better understand the world.  In examining these quantities, there are times when just a number, with a unit, can completely describe a situation.  These numbers, which have a magnitude, or size, only are known as scalars.  Examples of scalars include quantities such as temperature, mass, and time.  At other times, a quantity is more descriptive if it also includes a direction.  These quantities which have both a magnitude and direction are known as vectors.  Vector quantities you may be familiar with include force, velocity, and acceleration.

Most students will be familiar with scalars, but to many, vectors may be a new and confusing concept.  By learning just a few rules for dealing with vectors, though, you’ll find that they are a powerful tool for problem solving.

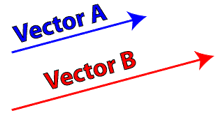
Vectors are often represented as arrows, with the length of the arrow indicating the magnitude of the quantity, and the direction of the arrow indicating the direction of the vector.  In the figure at right, vector B has a magnitude greater than that of vector A.  Vectors A and B point in the same direction, however.  It’s also important to note that vectors can be moved anywhere in space.  The positions of A and B could be reversed, and the individual vectors would retain their values of magnitude and direction.  This makes adding vectors very straightforward!

To add vectors A and B, all we have to do is line them up so that the tip of the first vector touches the tail of the second vector.  Then, to find the sum of the vectors, known as the resultant, all we have to do is draw a straight line from the start of the first vector to the end of the last vector.  This method works with any number of vectors.

 

So then, how do we subtract two vectors?  Let’s try it by subtracting B from A. We could rewrite the expression A - B as A + -B.  Now it becomes an addition problem, we just have to figure out how to express –B.  This is easier than it sounds – to find the opposite of a vector, we just point the vector in the opposite direction.  Therefore, we can use what we already know about the addition of vectors to find the resultant of A-B.

 

Components of Vectors

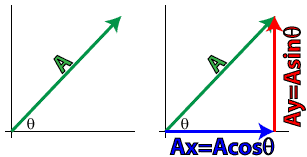
We'll learn more about vectors as we go, but before we move on, there are a few basic skills we need to learn. Vectors at angles can be challenging to deal with. By transforming a vector at an angle into two vectors, one parallel to the x-axis and one parallel to the y-axis, we can greatly simplify problem solving. To break a vector up into its components, we can use our basic trig functions.

 

In similar fashion, we can use the components of a vector in order to build the original vector. Graphically, if we line up the component vectors tip-to-tail, the original vector runs from the starting point of the first vector to the ending point of the last vector. To determine the magnitude of the resulting vector algebraically, just apply the Pythagorean Theorem.

Question: A motorboat, which has a speed of 5.0 meters per second in still water, is headed east as it crosses a river flowing south at 3.3 meters per second. What is the magnitude of the boat's resultant velocity with respect to the starting point?

1. 3.3 m/s
2. 5.0 m/s
3. 6.0 m/s
4. 8.3 m/s

Answer: (3) 6.0 m/s. The motorboat's resultant velocity is the vector sum of the motorboat's speed and the riverboat's speed.

 

Question: A 5.0-newton force could have perpendicular components of

1. 1.0 N and 4.0 N
2. 2.0 N and 3.0 N
3. 3.0 N and 4.0 N
4. 5.0 N and 5.0 N

Answer: (3) The only answers that fit the Pythagorean Theorem are 3.0 N and 4.0 N (3²+4²=5²)

 

Equilibrant Vector

The equilibrant of a force vector or set of force vectors is a single force vector which is exactly equal in magnitude and opposite in direction to the original vector or sum of vectors. The equilibrant, in effect, "cancels out" the original vector(s), or brings the set of vectors into equilibrium. To find an equilibrant, first find the resultant of the original vectors. The equilibrant is the opposite of the resultant you found!

Question: The diagram below represents two concurrent forces.

Which vector represents the force that will produce equilibrium with these two forces?

Answer: (3) The resultant of the two vectors would point up and to the left, therefore the equilibrant must point in the opposite direction, down and to the right.