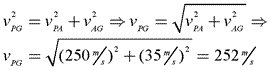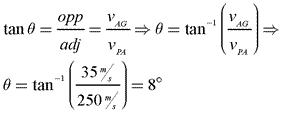Relative Velocity
Relative Motion
You’ve probably heard the saying “motion is relative.” Or perhaps you’ve heard people speak about Einstein’s Theory of General Relativity and Einstein’s Theory of Special Relativity. But what is this relativity concept?
In short, the concept of relative motion or relative velocity is all about understanding frame of reference. A frame of reference can be thought of as the state of motion of the observer of some event. For example, if you’re sitting on a lawnchair watching a train travel past you from left to right at 50 m/s, you would consider yourself in a stationary frame of reference. From your perspective, you are at rest, and the train is moving. Further, assuming you have tremendous eyesight, you could even watch a glass of water sitting on a table inside the train move from left to right at 50 m/s.

An observer on the train itself, however, sitting beside the table with the glass of water, would view the glass of water as remaining stationary from their frame of reference. Because that observer is moving at 50 m/s, and the glass of water is moving at 50 m/s, the observer on the train sees no motion for the cup of water.
This seems like a simple and obvious example, yet when you take a step back and examine the bigger picture, you quickly find that all motion is relative. Going back to our original scenario, if you’re sitting on your lawnchair watching a train go by, you believe you’re in a stationary reference frame. The observer on the train looking out the window at you, however, sees you moving from right to left at 50 m/s.
Even more intriguing, an observer outside the Earth’s atmosphere traveling with the Earth could use a “magic telescope” to observe you sitting in your lawnchair moving hundreds of meters per second as the Earth rotates about its axis. If this observer were further away from the Earth, he or she would also observe the Earth moving around the sun at speeds approaching 30,000 m/s. If the observer were even further away, they would observe the solar system (with the Earth, and you, on your lawnchair) orbiting the center of the Milky Way Galaxy at speeds approaching 220,000 m/s. And it goes on and on.
According to the laws of physics, there is no way to distinguish between an object at rest and an object moving at a constant velocity in an inertial (non-accelerating) reference frame. This means that there really is no “correct answer” to the question “how fast is the glass of water on the train moving?” You would be correct stating the glass is moving 50 m/s to the right and also correct in stating the glass is stationary. Imagine you’re on a very smooth airplane, with all the window shades pulled down. It is physically impossible to determine whether you’re flying through the air at a constant 300 m/s or whether you’re sitting still on the runway. Even if you peeked out the window, you still couldn’t say whether the plane was moving forward at 300 m/s, or the Earth was moving underneath the plane at 300 m/s.
As you observe (pun intended), how fast you are moving depends upon the observer’s frame of reference. This is what is meant by the statement “motion is relative.” In order to determine an object’s velocity, you really need to also state the reference frame (i.e. the train moves 50 m/s with respect to the ground; the glass of water moves 50 m/s with respect to the ground; the glass of water is stationary with respect to the train.)

In most instances, the Earth makes a terrific frame of reference for physics problems. However, there are times when calculating the velocity of an object relative to different reference frames can be useful. Imagine you’re in a canoe race, traveling down a river. It could be important to know not only your speed with respect to the flow of the river, but also your speed with respect to the riverbank, and even your speed with respect to your opponent’s canoe in the race.
In dealing with these situations, you can state the velocity of an object with respect to its reference frame. For example, the velocity of object A with respect to reference frame C would be written as vAC. Even if you don’t know the velocity of object A with respect to C directly, by finding the velocity of object A with respect to some intermediate object B, and the velocity of object B with respect to C, you can combine your velocities using vector addition to obtain:
This sounds more complicated than it actually is. Let's look at how this is applied in a few examples.
1-D Sample Problem
Question: A train travels at 60 m/s to the east with respect to the ground. A businessman on the train runs at 5 m/s to the west with respect to the train. Find the velocity of the man with respect to the ground.
Answer: First determine what information you are given. Calling east the positive direction, you know the velocity of the train with respect to the ground (vTG=60 m/s). You also know the velocity of the man with respect to the train (vMT=-5 m/s). Putting these together, you can find the velocity of the man with respect to the ground.
2-D Sample Problem
This strategy isn't limited to one-dimensional problems. Treating velocities as vectors, you can use vector addition to solve problems in multiple dimensions.
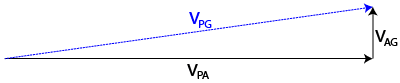
Question: The president’s airplane, Air Force One, flies at 250 m/s to the east with respect to the air. The air is moving at 35 m/s to the north with respect to the ground. Find the velocity of Air Force One with respect to the ground.
Answer: In this case, it’s important to realize that both vPA and vAG are two-dimensional vectors. You can find vPG by vector addition.
Drawing a diagram can be of tremendous assistance in solving this problem.
Looking at the diagram, you can easily solve for the magnitude of the velocity of the plane with respect to the ground using the Pythagorean Theorem.
You can find the angle of Air Force One using basic trig functions.
Therefore, the velocity of Air Force One with respect to the ground is 252 m/s at an angle of 8° north of east.