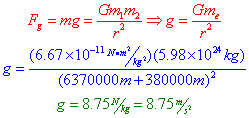Gravity
Universal Gravitation
All objects that have mass attract each other with a gravitational force. The magnitude of that force, Fg, can be calculated using Newton's Law of Universal Gravitation:
This law tells us that the force of gravity between two objects is proportional to each of the masses(m1 and m2) and inversely proportional to the square of the distance between them (r). The universal gravitational constant, G, is a "fudge factor," so to speak, included in the equation so that your answers come out in S.I. units. G is given as ![]() .
.
Let's look at this relationship in a bit more detail. Force is directly proportional to the masses of the two objects, therefore if either of the masses were doubled, the gravitational force would also double. In similar fashion, if the distance between the two objects, r, was doubled, the force of gravity would be quartered since the distance is squared in the denominator. This type of relationship is called an inverse square law, which describes many phenomena in the natural world.
NOTE: the distance between the masses, r, is actually the distance between the center of masses of the objects. For large objects, such as the Earth, for example, you must determine the distance to the center of the Earth, not to its surface.
Some hints for problem solving when dealing with Newton's Law of Universal Gravitation:
- Substitute values in for variables at the very end of the problem only. The longer you can keep the formula in terms of variables, the fewer opportunities for mistakes.
- Before using your calculator to find an answer, try to estimate the order of magnitude of the answer. Use this to check your final answer.
- Once your calculations are complete, make sure your answer makes sense by comparing your answer to a known or similar quantity. If your answer doesn't make sense, check your work and verify your calculations.
Let's see if we can't apply Newton's Law of Universal Gravitation to a simple problem...
Question: What is the gravitational force of attraction between two asteroids in space, each with a mass of 50,000 kg, separated by a distance of 3800 m?
Answer:
As you can see, the force of gravity is a relatively weak force, and we would expect a relatively weak force between relatively small objects. It takes tremendous masses and small distances in order to develop significant gravitational forces. Let's take a look at another problem to explore the relationships between gravitational force, mass, and distance.
Gravitational Fields
Gravity is a non-contact, or field, force. Its effects are observed without the two objects coming into contact with each other. Exactly how this happens is a mystery to this day, but scientists have come up with a mental construct to help us understand how gravity works.
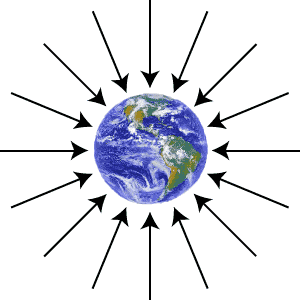
Envision an object with a gravitational field, such as the planet Earth. The closer other masses are to Earth, the more gravitational force they will experience. We can characterize this by calculating the amount of force the Earth will exert per unit mass at various distances from the Earth. Obviously, the closer the object is to the Earth, the larger a force it will experience, and the farther it is from the Earth, the smaller a force it will experience.
Attempting to visualize this, picture the strength of the gravitational force on a test object represented by a vector at the position of the object. The denser the force vectors are, the stronger the force, the stronger the "gravitational field." As these field lines become less and less dense, the gravitational field gets weaker and weaker.
To calculate the gravitational field strength at a given position, we can go back to our definition of the force of gravity on our test object, better known as its weight. We've been writing this as mg since we began our study of dynamics. But, realizing that this is the force of gravity on an object, we can also calculate the force of gravity on test mass using Newton's Law of Universal Gravitation. Putting these together we find that:
Realizing that the mass on the left-hand side of the equation, the mass of our test object, is also one of the masses on the right-hand side of the equation, we can simplify our expression by dividing out the test mass.
Therefore, the gravitational field strength, g, is equal to the universal gravitational constant, G, times the mass of the object, divided by the square of the distance between the objects.
But wait, you might say... I thought g was the acceleration due to gravity on the surface of the Earth! And you would be right. Not only is g the gravitational field strength, it's also the acceleration due to gravity. The units even work out... the units of gravitational field strength, N/kg, are equivalent to the units for acceleration, m/s2!
Still skeptical? Let's calculate the gravitational field strength on the surface of the Earth, using the knowledge that the mass of the Earth is approximately 5.98*1024 kg, and the distance from the surface to the center of mass of the Earth (which varies slightly since the Earth isn't a perfect sphere) is approximately 6378 km in New York.
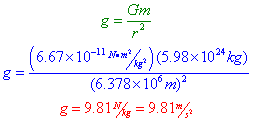
As expected, the gravitational field strength on the surface of the Earth is the acceleration due to gravity. Let's see if we can't solve some problems using gravitational field strength.
Question: Suppose a 100-kg astronaut feels a gravitational force of 700N when placed in the gravitational field of a planet.
A) What is the gravitational field strength at the location of the astronaut?
B) What is the mass of the planet if the astronaut is 2*106 m from its center?
Answer:
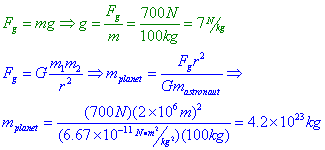
Orbits
How do celestial bodies orbit each other? The moon orbits the Earth. The Earth orbits the sun. Our solar system is in orbit in the Milky Way galaxy... but how does it all work?
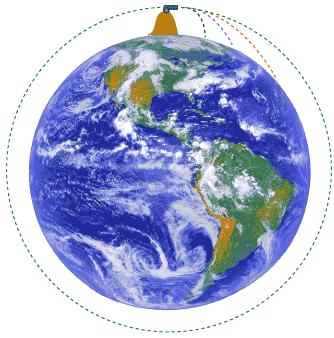
To explain orbits, Sir Isaac Newton developed a "thought experiment" in which he imagined a cannon placed on top of a very tall mountain, so tall, in fact, that the peak of the mountain was above the atmosphere (this is important because it allows us to neglect air resistance). If the cannon then launched a projectile horizontally, the projectile would follow a parabolic path to the surface of the Earth.
If the projectile was launched with a higher speed, however, it would travel farther across the surface of the Earth before reaching the ground. If its speed could be increased high enough, the projectile would fall at the same rate the Earth's surface curves away. The projectile would continue falling forever as it circled the Earth! This circular motion describes an orbit.
Put another way, the astronauts in the Space Shuttle aren't weightless. Far from it, actually, the Earth's gravity is still acting on themand pulling them toward the center of the Earth with a substantial force. We can even calculate that force. If the Space Shuttle orbits the Earth at an altitude of 380,000m, what is the gravitational field strength due to the Earth?
Question: If the Space Shuttle orbits the Earth at an altitude of 380 km, what is the gravitational field strength due to the Earth?
Answer: Recall that we can obtain values for G, the mass of the Earth, and the radius of the Earth from the reference table.
This means that the acceleration due to gravity at the altitude the astronauts are orbiting the earth is only 11% less than on the surface of the Earth! In actuality, the Space Shuttle is falling, but it's moving so fast horizontally that by the time it falls, the Earth has curved away underneath it so that the shuttle remains at the same distance from the center of the Earth -- it is in orbit. Of course, this takes tremendous speeds... to maintain an orbit of 380 km, the space shuttle travels approximately 7680 m/s, more than 23 times the speed of sound at sea level!