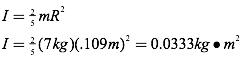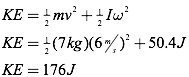Honors Physics - Rotational Kinetic Energy

Kinetic Energy

When kinematics was first introduced, kinetic energy was defined as the abil- ity of a moving object to move another object. Then, translational kinetic energy for a moving object was calculated using the formula:

 

Since an object which is rotating also has the ability to move another object, it, too, must have kinetic energy. Rotational kinetic energy can be calculated using the analog to the translational kinetic energy formula -- all you have to do is replace inertial mass with moment of inertia, and translational velocity with angular velocity!

 

If an object exhibits both translational motion and rotational motion, the total kinetic energy of the object can be found by adding the translational kinetic energy and the rotational kinetic energy:

 

Because you’re solving for energy, of course the answers will have units of Joules.

 

Question: Gina rolls a bowling ball of mass 7 kg and radius 10.9 cm down a lane with a velocity of 6 m/s. Find the rotational kinetic energy of the bowling ball, assuming it does not slip.

Answer: To find the rotational kinetic energy of the bowling ball, you need to know its moment of inertia and its angular velocity. Assume the bowling ball is a solid sphere to find its moment of inertia.

Next, find the ball’s angular velocity.

Finally, solve for the rotational kinetic energy of the bowling ball.

 

Question: Find the total kinetic energy of the bowling ball from the previous problem.

Answer: The total kinetic energy is the sum of the translational kinetic energy and the rotational kinetic energy of the bowling ball.

 

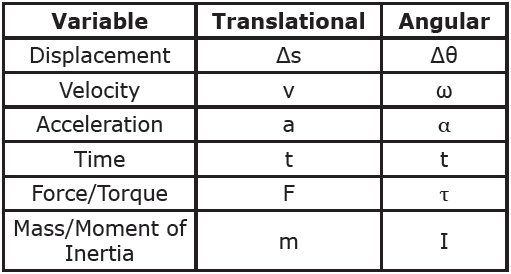
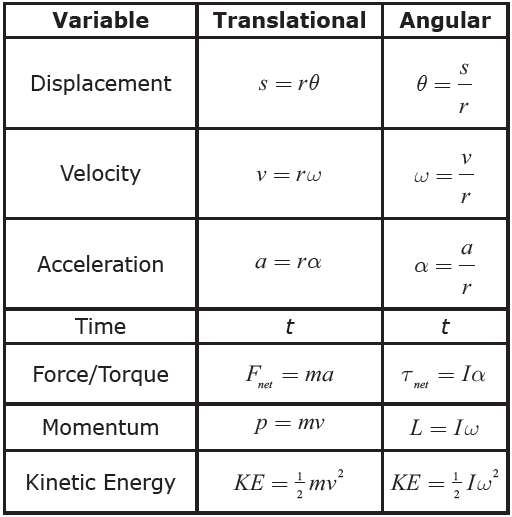
Formula Equivalencies

Putting all this information together, rotational physics mirrors translational physics in terms of both variables and formulas. These equivalencies and relationships are summarized below.