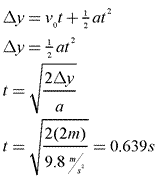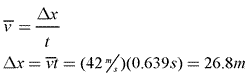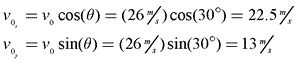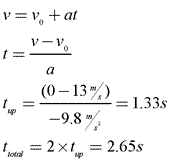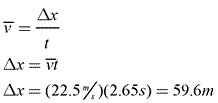A Plus Physics

Projectile Motion

General Strategy

Projectile motion problems, or problems of an object launched in both the x- and y- directions, can be analyzed using the physics you already know. The key to solving these types of problems is realizing that the horizontal component of the object’s motion is independent of the vertical component of the object’s motion. Since you already know how to solve horizontal and vertical kinematics problems, all you have to do is put the two results together!

Start these problems by making separate motion tables for vertical and horizontal motion. Vertically, the setup is the same for projectile motion as it is for an object in free fall. Horizontally, gravity only pulls an object down, it never pulls or pushes an object horizontally, therefore the horizontal acceleration of any projectile is zero. If the acceleration horizontally is zero, velocity must be constant, therefore v0 horizontally must equal v horizontally. Finally, to tie the problem together, realize that the time the projectile is in the air vertically must be equal to the time the projectile is in the air horizontally.

 

Horizontal Projectiles

When an object is launched or thrown completely horizontally, such as a rock thrown horizontally off a cliff, the initial velocity of the object is its initial horizontal velocity. Because horizontal velocity doesn’t change, this velocity is also the object’s final horizontal velocity, as well as its average horizontal velocity. Further, the initial vertical velocity of the projectile is zero. This means that you could hurl an object 1000 m/s horizontally off a cliff, and simultaneously drop an object off the cliff from the same height, and they will both reach the ground at the same time (even though the hurled object has traveled a greater distance).

Baseball Player

Question: Fred throws a baseball 42 m/s horizontally from a height of 2m. How far will the ball travel before it reaches the ground?

Answer: To solve this problem, you must first find how long the ball will remain in the air. This is a vertical motion problem.

Fred baseball time solution
  • v0=0 m/s
  • v=?
  • Δy=2m
  • a=9.8 m/s2
  • t=?

 

 

 

Now that you know the ball is in the air for 0.639 seconds, you can find how far it travels horizontally before reaching the ground. This is a horizontal motion problem, in which the acceleration is 0 (nothing is causing the ball to accelerate horizontally.) Because the ball doesn’t accelerate, its initial velocity is also its final velocity, which is equal to its average velocity.

Fred baseball range
  • v0=42 m/s
  • v=42 m/s
  • Δx=?
  • a=0
  • t=0.639s

You can therefore conclude that the baseball travels 26.8 meters horizontally before reaching the ground.

 

 

Question: Projectile A is launched horizontally at a speed of 20 meters per second from the top of a cliff and strikes a level surface below, 3.0 seconds later. Projectile B is launched horizontally from the same location at a speed of 30 meters per second. The time it takes projectile B to reach the level surface is:

Answer: 3 seconds. They both take the same time to reach the ground because they both travel the same distance vertically, and they both have the same vertical acceleration (9.8 m/s2 down) and initial vertical velocity (zero).

 


Angled Projectiles

For objects launched at an angle, you have to do a little more work to determine the initial velocity in both the horizontal and vertical directions.  For example, if a football is kicked with an initial velocity of 40 m/s at an angle of 30° above the horizontal, you need to break the initial velocity vector up into x- and y-components in the same manner as covered in the components of vectors math review section.

Then, use the components for your initial velocities in your horizontal and vertical tables.  Finally, don't forget that symmetry of motion also applies to the parabola of projectile motion.  For objects launched and landing at the same height, the launch angle is equal to the landing angle.  The launch velocity is equal to the landing velocity.  And if you want an object to travel the maximum possible horizontal distance (or range), launch it at an angle of 45°.

Human Cannonball

Question: Herman the human cannonball is launched from level ground at an angle of 30° above the horizontal with an initial velocity of 26 m/s. How far does Herman travel horizontally before reuniting with the ground?

Answer: Our first step in solving this type of problem is to determine Herman's initial horizontal and vertical velocity. We do this by breaking up his initial velocity into vertical and horizontal components:

Components

Next, we'll analyze Herman's vertical motion to find out how long he is in the air. We'll analyze his motion on the way up, find the time, and double that to find his total time in the air:

Herman Time Calculation
  • v0=13 m/s
  • v=0
  • Δy=?
  • ay=-9.8 m/s2
  • t=?

Now that we know Herman was in the air 2.65s, we can find how far he moved horizontally, using his initial horizontal velocity of 22.5 m/s.

Herman Answer
  • v0=22.5 m/s
  • v=22.5 m/s
  • Δx=?
  • ax=0
  • t=2.65s

Therefore, Herman must have traveled 59.6m horizontally before returning to the Earth.

 

 

Question: A golf ball is hit at an angle of 45° above the horizontal. What is the acceleration of the golf ball at the highest point in its trajectory? [Neglect friction.]

Answer: 9.8 m/s2 downward