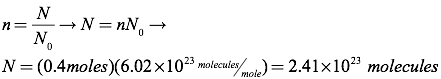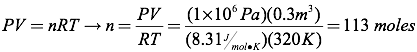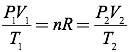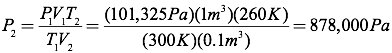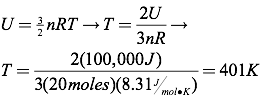Ideal Gas Law
In studying the behavior of gases in confined spaces, it is useful to limit ourselves to the study of ideal gases. Ideal gases are theoretical models of real gases, which utilize a number of basic assumptions to simplify their study. These assumptions include treating the gas as being comprised of many particles which move randomly in a container. The particles are, on average, far apart from one another, and they do not exert forces upon one another unless they come in contact in an elastic collision.
Under normal conditions such as standard temperature and pressure, most gases behave in a manner quite similar to an ideal gas. Heavy gases as well as gases at very low temperatures or very high pressures are not as well modeled by an ideal gas.
The Ideal Gas Law relates the pressure, volume, number of particles, and temperature of an ideal gas in a single equation, and can be written in a number of different ways.
In this equation, P is the pressure of the gas (in Pascals), V is the volume of the gas (in cubic meters), n is the number of moles of gas, N is the number of molecules of gas, R is the universal gas constant equal to 8.31 J/mol·K (which is also 0.08206 L·atm/mol·K), kB is Boltzmann’s Constant (1.38×10-23 J/K), and T is the temperature, in Kelvins. To convert from molecules to moles, you can use Avogadro’s Number (N0=6.02×10-23 molecules/mole):
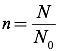
Note that a Pascal multiplied by a cubic meter is a newton-meter, or Joule. As well, Boltzmann’s constant is the ideal gas law constant divided by Avogadro’s number.
Question: How many moles of an ideal gas are equivalent to 3.01×1024 molecules?
Answer:
Question: Find the number of molecules in 0.4 moles of an ideal gas.
Answer:
Question: How many moles of gas are present in a 0.3 m3 bottle of carbon dioxide held at a temperature of 320K and a pressure of 1×106 Pascals?
Answer:
Question: A cubic meter of carbon dioxide gas at room temperature (300K) and atmospheric pressure (101,325 Pa) is compressed into a volume of 0.1 m3 and held at a temperature of 260K. What is the pressure of the compressed carbon dioxide?
Answer: Since the number of moles of gas is constant, you can simplify the ideal gas equation into the combined gas law by setting the initial pressure, volume, and temperature relationship equal to the final pressure, volume, and temperature relationship.
Since you know all the quantities in this equation except for the final pressure, you can solve for the final pressure directly.
Question: One mole of helium gas is placed inside a balloon. What is the pressure inside the balloon when the balloon rises to a point in the atmosphere where the temperature is -12°C and the volume of the balloon is 0.25 cubic meters?
Answer: First you must convert the temperature from degrees Celsius to Kelvins.
Next, you can use the ideal gas law to solve for the pressure inside the balloon.
It’s also quite straightforward to find the total internal energy of an ideal gas. Recall that the average kinetic energy of the particles of an ideal gas are described by the formula:
The total internal energy of an ideal gas can be found by multiplying the average kinetic energy of the gas’s particles by the number of particles (N) in the gas. Therefore, the internal energy of the gas can be calculated using:
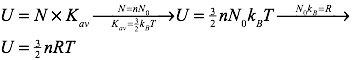
Question: Find the internal energy of 5 moles of oxygen at a temperature of 300K.
Answer:
Question: What is the temperature of 20 moles of argon with a total internal energy of 100 kJ?
Answer: