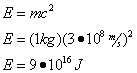Mass-Energy Equivalence
In 1905, in a paper titled "Does the Inertia of a Body Depend Upon Its Energy Content," Albert Einstein proposed the revolutionary concept that an object's mass is a measure of how much energy that object contains, opening a door to a host of world-changing developments, eventually leading us to the major understanding that the source of all energy in the universe is, ultimately, the conversion of mass into energy!
Conservation Laws
If mass is a measure of an object's energy, we need to re-evaluate our statements of the law of conservation of mass and the law of conservation of energy. Up to this point, we have thought of these as separate statements of fact in the universe. Based on Einstein's discovery, however, mass and energy are two concepts effectively describing the same thing, therefore we could more appropriately combine these two laws into a single law, the law of conservation of mass-energy, which states that mass-energy cannot be created nor destroyed.
The concept of mass-energy is one that is often misunderstood and oftentimes argued in terms of semantics... for example, a popular argument states that the concept of mass-energy equivalence means that mass can be converted to energy, and energy can be converted to mass. Many would disagree that this can occur, countering that since mass and energy are effectively the same thing, you can't convert one to the other. For our purposes, we'll save these arguments for future courses of study, and instead focus on a basic conceptual understanding.
The universal conservation laws we have studied so far this course include:
- Conservation of Mass-Energy
- Conservation of Charge
- Conservation of Momentum

E=mc2
Einstein's famous formula, E=mc2, relates the amount of energy contained in matter to the mass times the speed of light in a vacuum (c=3*108 m/s) squared. Theoretically, then, we could determine the amount of energy represented by 1 kilogram of matter as follows:
Question: What is the energy equivalent of 1 kilogram of matter?
Answer:

This is a very large amount of energy... to put it in perspective, the energy equivalent of a large pickup truck is in the same order of magnitude of the total annual energy consumption of the United States!
More practically, however, it is not realistic to convert large quantities of mass completely into energy. Current practice revolves around converting small amounts of mass into energy in nuclear processes. Typically these masses are so small that measuring in units of kilograms isn't practical. Instead, scientists often work with the much smaller universal mass unit (u), which is equal in mass to one-twelfth the mass of a single atom of Carbon-12. The mass of a proton and neutron, therefore, is close to 1u, and the mass of an electron is close to 5*10-4 u. In precise terms, 1u=1.66053886*10-27 kg.
One universal mass unit (1u) completely converted to energy is equivalent to 931 MeV. Because mass and energy are different forms of the same thing, this could even be considered a unit conversion problem. If given a mass in universal mass units, you can use this equivalence directly to solve for the equivalent amount of energy, without having to convert into standard units and utilize the E=mc2 equation.
Question: If a deuterium nucleus has a mass of 1.53*10-3 universal mass units (u) less than its components, how much energy does its mass represent?
Answer:
Binding Energy
The nucleus of an atom consists of positively charged protons and neutral neutrons. Collectively, these nuclear particles are known as nucleons. Protons repel each other electrically, so why doesn't the nucleus fly apart? There is another force which holds nucleons together, known as the strong nuclear force. This extremely strong force overcomes the electrical repulsion of the protons, but it is only effective over very small distances.
Because nucleons are held together by the strong nuclear force, you must add energy to the system to break apart the nucleus. The energy required to break apart the nucleus is known as the binding energy of the nucleus.
If measured carefully, we find that the mass of a stable nucleus is actually slightly less than the mass of its indivudal component nucleons. The difference in mass between the entire nucleus and the sum of its component parts is known as the mass defect (Δm). The binding energy of the nucleus, therefore, must be the energy equivalent of the mass defect due to the law of conservation of mass-energy: Ebinding=mc2.
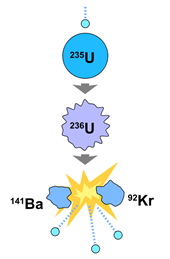
Fission & Fusion
Fission is the process in which a nucleus splits into two or more nuclei. For heavy (larger) nuclei such as Uranium-235, the mass of the original nucleus is greater than the sum of the mass of the fission products. Where did this mass go? It is released as energy! A commonly used fission reaction involves shooting a neutron at an atom of Uranium-235, which briefly becomes Uranium-236, an unstable isotope. The Uranium-236 atom then fissions into a Barium-141 atom and a Krypton-92 atom, releasing its excess energy while also sending out three more neutrons to continue a chain reaction! This process is responsible for our nuclear power plants, and is also the basis (in an uncontrolled reaction) of atomic fission bombs.
Fusion, on the other hand, is the process of combining two or more smaller nuclei into a larger nucleus. If this occurs with small nuclei, the product of the reaction may have a smaller mass its precursors, thereby releasing energy as part of the reaction. This is the basic nuclear reaction that fuels our sun and the stars as hydrogen atoms combine to form helium. This is also the basis of atomic hydrogen bombs.
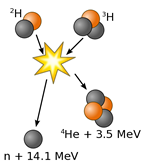
Nuclear fusion holds tremendous potential as a clean source of power with widely available source material (we can create hydrogen from water). The most promising fusion reaction for controlled energy production fuses two isotopes of hydrogen known as deuterium and tritium to form a helium nucleus and a neutron, as well as an extra neutron, while releasing a considerable amount of energy. Currently, creating a sustainable, controlled fusion reaction that outputs more energy than is required to start the reaction has not yet been demonstrated, but remains an area of focus for scientists and engineers.
Question: After a uranium nucleus emits an alpha particle, the total mass of the new nucleus and the alpha particle is less than the mass of the original uranium nucleus. Explain what happens to the missing mass.
Answer: The missing mass is converted into energy.