Reflection

When a wave hits a boundary, three different events can occur. The wave may be:

• Reflected - wave bounces off a boundary
• Transmitted - wave is transmitted into the new medium
• Absorbed - energy of the wave is transferred into the boundary medium

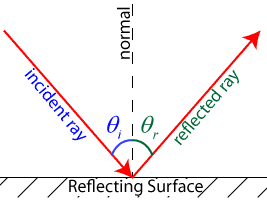
The law of reflection states that the angle at which a wave strikes a reflective medium (the angle of incidence, or θ_i) is equal to the angle at which a wave reflects off the medium (the angle of reflection, or θ_r). Put more simply, θ_i=θ_r. In all cases, the angle of incidence and the angle of reflection are measured from a line perpendicular, or normal, to the reflecting surface.

Although all waves can exhibit these behaviors, electromagnetic light waves are typically considered for demonstration purposes. When a wave bounces off a reflective surface, the nature of its reflection depends largely on the nature of the surface. Rough surfaces tend to reflect light in a variety of directions in a process known as diffuse reflection. Diffuse reflection is the type of reflection typically observed off of pieces of paper. Smooth surfaces tend to reflect light waves in a more regular fashion, such that the reflected rays maintain parallel reflected rays. This process is known as specular reflection, and is commonly observed in mirrors.

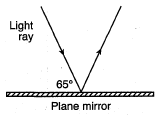
Question: The diagram represents a light ray reflecting from a plane mirror. Find the angle of reflection for the light ray.

Answer: The angle of reflection must be 25°, since the angle of incidence is 25° (note that angles are always measured from the normal!)

 

 

 

Mirrors

When you look in a flat (plane) mirror, you see a reflection, or an image, of an object. Light rays from the object reach the plane mirror and are reflected back to the observer, creating an image of the object. The image is known as a virtual image because the reflected rays don’t actually pass through the image. All virtual images are upright.

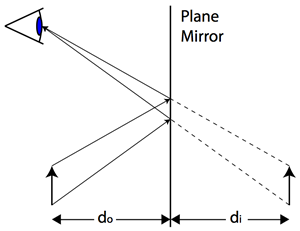
The distance from the object to the mirror is known as the object distance (d_o), and the distance from the image to the mirror is known as the image distance (d_i). For virtual images, the image distance is negative. The magnification of an image can be found using the magnification equation, which relates the image and object distances to the image (h_i) and object (h_o) heights.

In the case of a plane mirror, the magnitude of the image distance is equal to the magnitude of the object distance, therefore the image appears the same size as the object.

 

Question: A student stands 2 meters in front of a vertical plane mirror. As the student walks toward the mirror, the image

1. decreases in magnification and remains virtual
2. decreases in magnification and remains real
3. remains the same magnification and remains virtual
4. remains the same magnification and remains real

Answer: (3) remains the same magnification and remains virtual since the image stays behind the reflecting surface, and the magnification of a plane mirror is always 1.

 

 

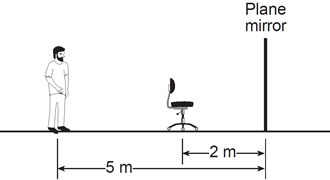
Question: In the diagram below, a person is standing 5 meters from a plane mirror. The chair in front of the person is located 2 meters from the mirror.

What is the distance between the person and the image he ob- serves of the chair?

Answer: 7m

 

 

Not all mirrors are plane mirrors, however. The inner surface of a spherical concave mirror is reflective. Light rays coming into a mirror parallel to the principal axis (a virtual line perpendicular to the mirror’s surface) are reflected from the plane of the mirror and converge through the focal point of the mirror. Concave mirrors are also known as converging mirrors. The focal point of a spherical mirror is half its radius of curvature.

Light rays passing through the center of curvature strike the mirror and are reflected back through the center of curvature. Light rays from the object passing directly through the focal point are reflected back parallel to the principal axis. The convergence of the reflected rays creates an image. The distance from the focal point to the mirror’s surface is known as the focal distance (f). The image is known as a real image because the reflected rays pass through the image. Real images are inverted.

 

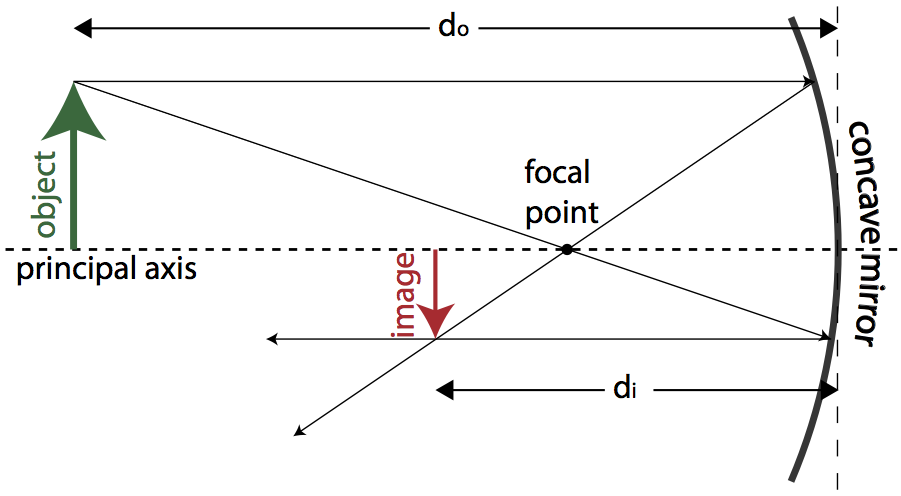
The relationship between the focal distance, the object distance, and the image distance is described by the mirror equation, also known as the lens-maker’s equation. By convention, object and image distances are positive on the reflecting side of the mirror, and negative on the non-reflecting side of the mirror.

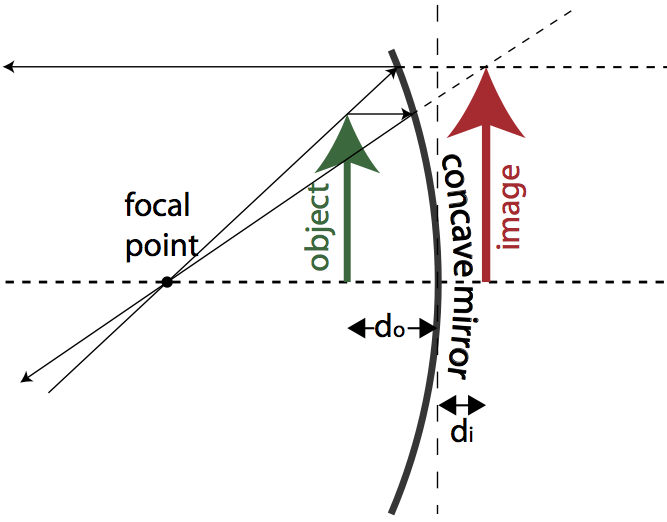
Analyzing an object inside the focal point of a concave mirror requires the same basic procedure. In this case, however, the reflected rays diverge on the reflective side of the mirror. To find the image, you must extend the real reflected rays back through the mirror onto the non-reflective side. The convergence of these extended rays leads to an upright, virtual image.

 

Question: An incident light ray travels parallel to the principal axis of a concave spherical mirror. After reflecting from the mirror, the light ray will travel

1. through the mirror’s focal point
2. through the mirror’s center of curvature
3. parallel to the mirror’s principal axis
4. normal to the mirror’s principal axis

Answer: (1) light rays parallel to the principal axis are reflected through the mirror’s focal point.

 

 

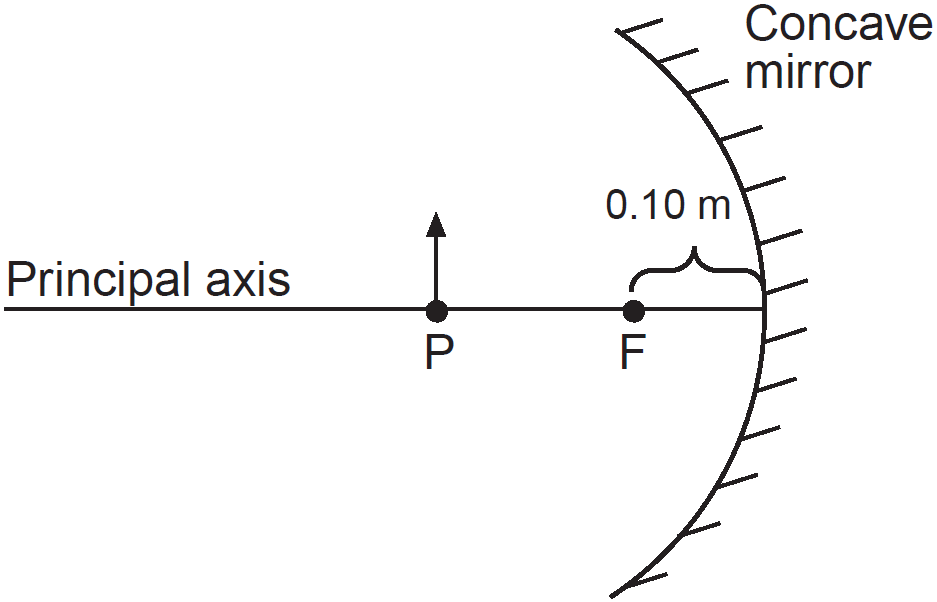
Question: The diagram below shows an object located at point P, 0.25 meters from a concave spherical mirror with focal point F. The focal length of the mirror is 0.10 meters.

How does the image change as the object moves from point P toward point F?

1. Its distance from the mirror decreases and the size of the image decreases.
2. Its distance from the mirror decreases and the size of the image increases.
3. Its distance from the mirror increases and the size of the image decreases.
4. Its distance from the mirror increases and the size of the image increases.

Answer: (4) Using the mirror equation below, you observe that by moving the object toward point F, the object distance d_o decreases.

Since the focal point f is fixed, the image distance d_i must increase, so the image’s distance from the mirror increases. Further, using the magnification equation, you observe that d_i increasing and d_o decreasing leads to an increase in magnification m.

 

 

The outer surface of a spherical convex mirror is reflective. Light rays coming into a convex mirror parallel to the principal axis are reflected away from the principal axis on a virtual line connecting the point of contact with the mirror plane and the focal point on the non-reflecting side of the mirror. For this reason, convex mirrors are also known as diverging mirrors. Light rays which strike the center of the mirror are reflected at the same angle. Because the light rays never converge on the reflective side of a convex mirror, convex mirrors only produce virtual images that are upright and reduced in size.

 

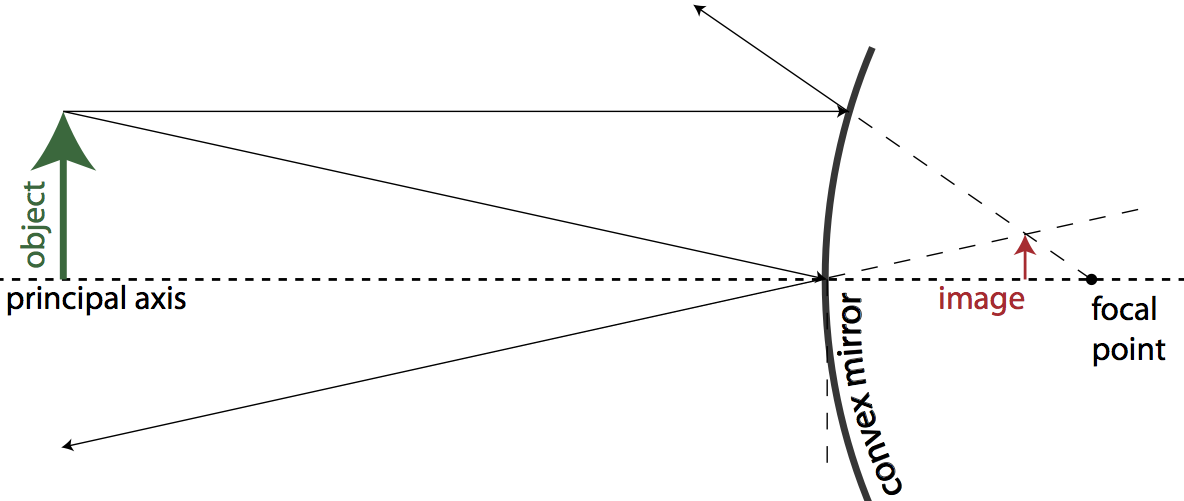
Question: Which optical device causes parallel light rays to diverge?

1. convex mirror
2. plane mirror
3. concave mirror
4. convex lens

Answer: (1) convex mirrors are also known as diverging mirrors.

 

 

Question: The radius of curvature of a spherical mirror is R. The focal length of this mirror is equal to

1. R/2
2. 2R
3. R/4
4. 4R

Answer: (1) The focal length of a mirror is equal to half its radius of curvature.